Sanoq sistemalari
Hozirgi kunda ishlatilib
kelayotgan 1, 2, 3,..., 9, 0 raqamdan iborat o'nlik sanoq sistemasi axborotni
kodlashning yana bir usuli hisoblanadi. Yurtdoshimiz Muhammad al-Xorazmiy 0
raqamini kiritib bu arab (to'g'rirog'i, hind) raqamlarining sondagi turgan
o'rniga bog'liq holda amallar bajarish tartibini yagona tizimga birlashtirgan.
Shuning uchun ham bu kodlash sistemasi ustida qo'shish, ayirish, ko'paytirish
va bo'lish kabi arifmetik amallarni bajarish juda oson.
Tarixiy ma'lumotlar
Odamlar o'rtasida muomala
vositasi bo'lmish til kabi sonlarning ham o'z tili mavjud bo'lib, u ham o'z
alifbosiga ega. Bu alifbo raqamlar va sonlami ifodalash uchun qo'llaniladigan
belgilardan iboratdir. Masalan, kundalik hayotimizda qo'llanadigan arab
raqamlari 1,2, …, 9, 0 yoki rim
raqamlari I, II, V, X, L, С, M, H, . . ., sonlar alifbosining elementlari
hisoblanadi. Turli davrlarda turli xalqlar, qabilalar raqamlar va sonlarni
ifodalashda turlicha belgilardan foydalanganlar. Masalan, qadimgi Misrda raqam
va sonlarni ifodalashda quyidagi belgilardan foydalanilgan:
Qadimgi meksikaliklar
(asteklar) esa 402 sonini quyidagicha belgilaganlar:
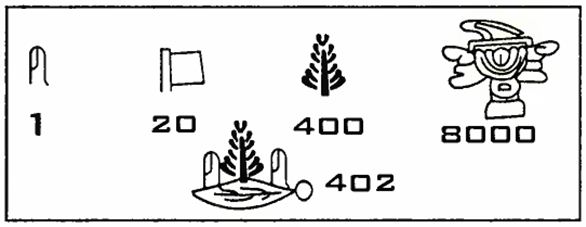
Qadimda ba'zi xalqlar
ishlatadigan sonlar alifbosi beshta (qadimgi Afrika qabilalarida), o'n ikkita
(masalan, inglizlarning sonlar alifbosida), yigirmata (XVI-XVII asrlarda
Amerika qit'asida yashagan astek, mayya qabilalarida; eramizdan avvalgi II
asrda G'arbiy Yevropada yashagan keltlarda; fransuzlarda), ba'zilari oltmishta
(qadimgi bobilliklarda) belgini o'z ichiga olgan. Ular
mos ravishda besh raqamli (qisqacha beshlik) sanoq sistemasi, o'n ikki raqamli
(o'n ikkilik) sanoq sistemasi, yigirmata raqamli (yigirmalik) sanoq sistemasi
yoki oltmishlik sanoq sistemasi deb nomlanadi.
Soatning
oltmishga,
sutkaning
o'n ikkiga karraliligi, bir yilning 12 oydan iboratligi, inglizlarda uzunlik o'lchov birligi bo'lmish 1 futning 12 dyumga tengligi, fransuzlarning
bir
franki
yigirma
suga
tengligi
turli
sanoq
sistemalarining
qo'llanilishi natijasidir. Inson har bir
sistemani ishlatganda ma'lum vositalardan ham foydalangan. Masalan, o'n ikkilik
sanoq sistemasi uchun vosita sifatida qo'l barmoqlaridagi bo'g'inlardan
foydalanilgan, biz kundalik hayotimizda qo'llayotgan sonlar alifbosi o'nta arab
raqamini o'z ichiga olgan bo'lib, uning
kelib chiqishida va qo'llanilishida tabiiy hisoblash vositasi bo'lmish qo'l
barmoqlarimiz
asosiy o'rin tutadi.
Sanoq sistemalari turlari
Ma'lumki, harflardan iborat
alifboni qollashda bir qancha qonun va qoidalarga amal qilinadi. Sonli
alifbodagi belgilardan foydalanishda ham o'ziga xos qoidalardan foydalaniladi.
Bu qoidalar turli alifbolar uchun turlicha bo'lib, mazkur alifboning kelib
chiqish tarixi bilan bog'liq. O'z ichiga o'nta raqamni olganligi uchun bu
alifbo o'zining barcha qoidalari bilan birgalikda o'n raqamli sanoq sistemasi
yoki qisqacha о
'nlik sanoq sistemasi deb ataladi.
Sonlar sistemasidagi
raqamlar soni shu sistemaning asosi deb yuritiladi.
Sonlar alifbosiga kiritilgan
(bir xonali) belgilar raqamlar va ular yordamida hosil qilingan boshqa (ko'p
xonali) belgilar sonlar deb yuritiladi. Masalan, o'nlik sanoq sistemasida 5, 6,
8 - bu raqamlar, ammo 568 - bu son. O'nlik sanoq sistemasida birliklar,
yuzliklar, mingliklar va boshqalar har biri o'ntadan belgilardan iborat guruhlarga
bo'lingan: 0, 1, ... , 9; 0 ta, 1 ta,..., 9 ta 10; 0 ta, 1 ta,..., 9 ta
100,.... Boshqa asosli sanoq sistemalardagi belgilar shu sistema asosi nechaga
teng bo'lsa, shuncha belgilardan iborat guruhlarga ajratiladi.
O'nlik sanoq sistemasida
raqamlar o'zi turgan o'rniga (razryadiga) ko'ra turlicha miqdorni anglatadi.
Masalan: a) 999: 9 (to'qqiz) - birlik; 90 (to'qson) -
o'nlik; 900 (to'qqiz yuz) - yuzlik;
b) 1991: 1 (bir) - birlik; 90 (to'qson) - o'nlik; 900
(to'qqiz yuz) - yuzlik; 1 (ming) - minglik.
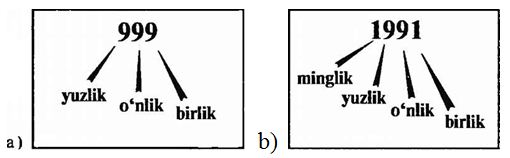
Shu bois ham bu sistema
raqamlari o'z pozitsiyasi (turgan o'rni) ga bog'liq bo'lgan sistema deb ham
yuritiladi.
Sanoq sistemalari shu
xossasiga ko'ra raqamlarining pozitsiyasiga bog’liq bo'lgan va raqamlarining
pozitsiyasiga bog'liq bo'lmagan sanoq sistemalariga (qisqacha pozitsiyali va
pozitsiyali bo'lmagan sanoq sistemalariga) bo'linadi. Pozitsiyali bolmagan
sanoq sistemasiga rim sanoq sistemasi misol bo'ladi.
Sizga ma'lumki, pozitsiyali
sanoq sistemasi bo'lgan o'nlik sanoq sistemasida arifmetik amallar bajarish
juda qulay, lekin, pozitsiyali bo'lmagan sanoq sistemasi bo'lgan rim sanoq sistemasida
arifmetik amallar bajarish juda murakkab. Shuning uchun ham ajdodlarimiz
raqamlar va sonlarni aniq bir shakllar tizimiga keltirish masalasiga katta
e'tibor qaratganlar.
Pozitsiyali sanoq
sistemalarida qo'llaniladigan qoidalar turlicha bo'lsada, ular bir xil tamoyil
asosida qurilgan. Mazkur tamoyilga ko'ra ixtiyoriy manfiy bo’lmagan N butun sonini p asosli sanoq sistemada quyidagicha ifodalash mumkin:
bu yerda:
-berilgan sonni tashkil etuvchi raqamlar (ularning qiymati p dan kichik);
k - sondagi raqamlar sonidan
bitta kam miqdor (chunki birinchi razryad 0 (nol) dan boshlangan).
Masalan, o'nlik sanoq
sistemasidagi 98327 sonida 7 raqami birlikni, 2 raqami o'nlikni. 3 raqami
yuzlikni, 8 raqami minglikni, 9 raqami o'n minglikni ifodalaydi.
Yuqoridagi ifodaga ko'ra
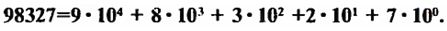
Pozitsiyali sanoq
sistemalariga ikkilik, sakkizlik va o'n oltilik sanoq sistemalari ham kiradi.
Ikkilik sanoq sistemasida 2 ta raqam mavjud: 0 va 1. Sakkizlik sanoq
sistemasida 8 ta raqam bor: 0, 1, 2, 3, 4, 5, 6, 7. Sonlarni o'n oltilik sanoq
sistemasida ifodalash uchun o'n oltita raqam: 0. 1,2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, E, F dan foydalaniladi. Bu yerda А, В, C, D, E, F raqamlarining qiymati mos ravishda o'nlik
sanoq sistemasidagi 10, 11, 12, 13, 14, 15 sonlarining qiymatiga tengdir. Ular
sonlardan farqlanishi uchun lotin harflari bilan belgilangan. Sakkizlik sanoq
sistemasida 8 soni, o'n oltilik sanoq sistemasida 16 soni 10 ko'rinishda
yoziladi.
Raqamni surish deganda uni
sonlar alifbosida o'zidan keyin kelgan raqamga almashtirish tushuniladi.
Masalan, 1 ni surishda 2 ga, 2 ni surishda 3 ga va hokazo almashtiriladi. Eng
katta raqamni surish (masalan, o'nlik sanoq sistemasidagi 9 ni) deganda 0 ga
almashtirish tushuniladi, bunda butun sonni oldiga yozilgan 0 uning qiymatiga
ta'sir etmasligi e'tiborga olinadi. Ikkilik sanoq sistemasida 0 ni surishda 1
ga, 1 ni surishda 0 ga almashtiriladi.
Pozitsiyali sanoq
sistemasida butun sonlarni quyidagi qonuniyat asosida hosil qilinadi: keyingi
son oldingi sonning o'ngdigi oxirgi raqamini surish orqali hosil qilinadi; agar
surishda biror raqam 0 ga aylansa, u holda bu raqamdan chapda turgan raqam
suriladi.
Shu qonuniyatdan foydalanib,
quyidagi birinchi 10 ta butun sonni hosil qilamiz:
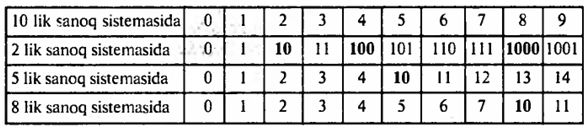
Jadvaldan ko'rinadiki, turli
sanoq sistemalarida o'xshash sonlar bor ekan. Shu sababli bu sonlarni farqlash
uchun informatikada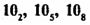 
kabi belgilash qabul qilingan.
Qisqacha tarixiy ma'lumot
Abu Abdulloh Muhammad ibn Muso al-Xorazmiy
Buyuk matematik, astronom va
geograf Muhammad al- Xorazmiy VIII asrning oxiri va IX asrning birinchi yarmida
yashab ijod etgan mutaffakir allomalardan biridir. Muso al-Xorazmiy (uning
to'liq ismi Abu Ja'far (Abu Abdulloh) Muhammad ibn Muso al-Xorazmiy) 783-yilda
Xorazmda tug'ilgan. Udastlabki ma'lumot va turli sohadagi bilimlarini asosan
o'z yurtida, O'rta Osiyo shaharlarida ijod etgan olimlar va mutafakkirlardan
olgan.
Manbalarda Xorazmiyning
ismiga yana al-Majusiy va Qutrubbuliy nomlari ham qo'shib aytladi.
Xorazmiyning qalamiga mansub
20 dan ortiq asarlarning faqat 10 tasi bizgacha yetib kelgan. Bular
"Al-jabr va al-muqobala hisobi haqida qisqacha kitob "(algebraik
asar); "Hind hisobi haqida kitob "yoki "Qo'shish va ayirish
haqida kitob "(arifmetik asar); "Kitob surat-ul-arz "
(geografiyaga oid asar); Zij ", "Asturlob bilan ishlash haqida kitob
", "Asturlob yasash haqida kitob ". "Asturlob yordamida azimutni
aniqlash haqida ", "Kitob ar-ruhoma ", "Kitob at-tarix
" (astronomiyaga oid asar). Bu asarlarning to'rttasi arab tilida, bittasi
Farg'oniyning asari tarkibida, ikkitasi lotincha tarjimada saqlangan va qolgan
uchtasi hali topilgan emas.
Xorazmiyning arifmetik
risolasi qachon yozilgani noma 'lum. Biroq unda olim algebraik risolasini
eslaydi. Demak, bundan Xorazmiy arifmetik risolasini
algebraik risoladan keyin yozgani ma'lum bo'ladi. Bu
risola XII asrda Ispaniyada lotin tiliga tarjima qilingan. Tarjimaning XIV
asrda ko'chirilgan yagona qo'lyozmasi Kembrij universiteti kutubxonasida
saqlanadi. Risola "Diksit Aggorizmi", ya'ni "Al-Xorazmiy aytdi
" iborasi bilan boshlanadi. Bundan keyin Xorazmiy to'qqizta hind raqamining
sonlarni ifodalashdagi afzalliklari va ular yordamida har qanday sonni ham qisqa
qilib va osonlik bilan yozish mumkinligini aytadi. Ayniqsa, nol (0)ni ishlatishning
ahamiyati haqida tushuncha berib, uni yozmaslik natijaning xato chiqishiga olib
keladi, degan edi.
Asarning lotincha
qo'lyozmasida hind raqamlari ko'pincha yozilmay, ulaming o'rni bo'sh
qoldirilgan yoki ahyon-ahyonda 1, 2, 3, 5 sonlarga mos keladigan hind raqamlari
yozilgan. Ba'zan esa hind raqamlari о'sha davrda Yevropada keng tarqalgan rim raqamlari
bilan almashtirilgan.
U shunday deydi: "...
Men arifmetikaning oddiy va murakkab masalalarini о 'z ichiga oluvchi "Al-jabr va al-muqobala hisobi
haqida qisqacha kitob" ni taklif qildim, chunki meros taqsim qilishda,
vasiyatnoma tuzishda, mulk taqsimlashda va adliya ishlarida savdoda va har
qanday bitimlarda, shuningdek, yer o'lchash, kanallar o'tkazishda, (amaliy) geometriya
va boshqa shunga o'xshash turlicha ishlarda kishilar uchun bu zarurdir".
